In many modern applications of machine learning, it is not out of ordinary to be dealing with data consisting of a large number of features. This high dimensionality of the feature space not only presents computational problems in the training of predictive models but also makes the learned model harder to interpret by human users. In this post we discuss a classical and traditionally important technique for reducing the feature dimension of a given dataset, called the Principal Component Analysis, or in short PCA. While still a widely used approach in general data analysis, as we will see PCA often performs relatively poorly for reducing the feature dimension of predictive modeling data. However, it does present a fundamental mathematical archetype, the matrix factorization, that provides a very useful way of organizing our thinking about a wide array of important learning models (including linear regression, K-means, Recommender Systems, etc.), all of which may be thought of as variations of the simple theme of matrix factorization.
# imports from custom library
import sys
sys.path.append('../../')
import matplotlib.pyplot as plt
import autograd.numpy as np
import math
import pandas as pd
%matplotlib notebook
# this is needed to compensate for %matplotlib notebook's tendancy to blow up images when plotted inline
from matplotlib import rcParams
rcParams['figure.autolayout'] = True
%load_ext autoreload
%autoreload 2
Principal Component Analysis (PCA) is a general approach to lowering the dimension of the feature space. It works by simply projecting the data onto a suitable lower dimensional feature subspace, that is one which hopefully preserves the essential geometry of the original data. This subspace is found by determining one of its spanning sets (e.g., a basis) of vectors which spans it. The basic setup is illustrated in the figure below.
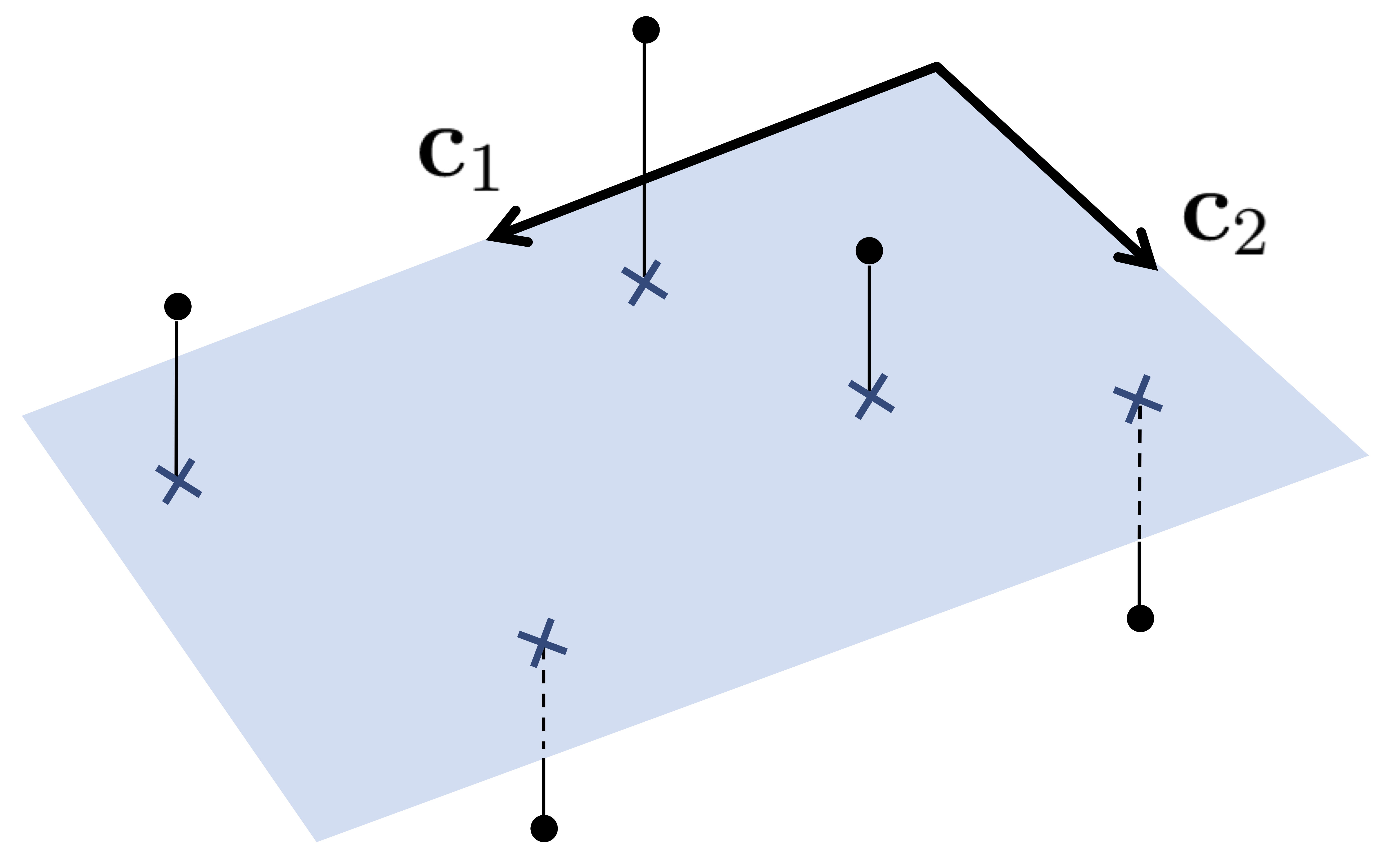
Suppose that we have $P$ data points $\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{P}$, each of dimension $N$. The goal with PCA is, for some user chosen dimension $K<N$, to find a set of $K$ vectors $\mathbf{c}_{1}, \mathbf{c}_{2}, \dots, \mathbf{c}_{K}$ that represent the data fairly well. Put formally, we want for each $p=1, 2, \ldots, P$ to have
\begin{equation} \underset{k=1}{\overset{K}{\sum}}\mathbf{c}_{k}w_{k,p}\approx\mathbf{x}_{p} \end{equation}Stacking the desired spanning vectors column-wise into the $N\times K$ matrix $\mathbf{C}$ as
\begin{equation} \mathbf{C}=\left[\begin{array}{cccc} \mathbf{c}_{1} & \mathbf{c}_{2} & \cdots & \mathbf{c}_{K}\end{array}\right] \end{equation}and denoting
\begin{equation} \mathbf{w}_{p}=\left[\begin{array}{c} w_{1,p}\\ w_{2,p}\\ \vdots\\ w_{K,p} \end{array}\right] \end{equation}this can be written equivalently for each $p$ as
\begin{equation} \mathbf{C}\mathbf{w}_{p}\approx\mathbf{x}_{p} \end{equation}Notice, once $\mathbf{C}$ and $\mathbf{w}_{p}$ are learned the new $K$ dimensional feature representation of $\mathbf{x}_{p}$ is then the vector $\mathbf{w}_{p}$ (i.e., the weights over which $\mathbf{x}_{p}$ is represented over the spanning set).
By denoting
\begin{equation} \mathbf{W}=\left[\begin{array}{cccc} \mathbf{w}_{1} & \mathbf{w}_{2} & \cdots & \mathbf{w}_{P}\end{array}\right] \end{equation}the $K\times P$ matrix of weights to learn, and
\begin{equation} \mathbf{X}=\left[\begin{array}{cccc} \mathbf{x}_{1} & \mathbf{x}_{2} & \cdots & \mathbf{x}_{P}\end{array}\right] \end{equation}the $N\times P$ data matrix, all $P$ of these approximate equalities in equations (1) and (4) can be written compactly as
\begin{equation} \mathbf{C}\mathbf{W}\approx\mathbf{X} \end{equation}The goal of PCA, compactly stated in equation (7), naturally leads to determining $\mathbf{C}$ and $\mathbf{W}$ by minimizing $\left\Vert \mathbf{C}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}$, i.e., by solving
\begin{equation} \begin{aligned}\underset{\mathbf{C},\mathbf{W}}{\mbox{minimize}} & \,\,\,\,\,\left\Vert \mathbf{C}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{equation}In this Example we show the result of applying PCA on two simple 2D datasets using a solution to the PCA problem in (8) that we derive in Subsection 1.2.
In the top panels dimension reduction via PCA retains much of the structure of the original data. Conversely, the more structured square data set loses much of its original characteristic after projection onto the PCA subspace as shown in the bottom panels.
While PCA can technically be used for preprocessing data in a predictive modeling scenario, it can cause severe problems in the case of classification. In this Example we illustrate feature space dimension reduction via PCA on a simulated two-class dataset where the two classes are linearly separable. Because the ideal one-dimensional subspace in this instance runs parallel to the longer length of each class, projecting the complete dataset onto it completely destroys the separability.
Digital image compression aims at reducing the size of digital images without adversely affecting their quality. Without compression a natural photo taken by a digital camera would require one to two orders of magnitude more storage space. As shown in the figure below, in a typical image compression scheme an input image is first cut up into small square (typically $8 \times 8$ pixel) blocks. The values of pixels in each block (which are integers between $0$ and $255$ for an 8-bit grayscale image) are stacked into a column vector $y$, and compression is then performed on these individual vectorized blocks.
The primary idea behind many digital image compression algorithms is that with the use of specific bases, we only need very few of their elements to very closely approximate any natural image. One such basis, the $8 \times 8$ discrete cosine transform (DCT) which is the backbone of the popular JPEG compression scheme, consists of two-dimensional cosine waves of varying frequencies, and is shown in the figure below along with its analogue standard basis.

Most natural image blocks can be well approximated using only a few elements of the DCT basis. The reason is, as opposed to bases with more locally defined elements (e.g., the standard basis), each DCT basis element represents a fluctuation commonly seen across the entirety of a natural image block. Therefore with just a few of these elements, properly weighted, we can approximate a wide range of image blocks. In other words, instead of seeking out a basis (as with PCA), here we have a fixed basis over which image data can be very efficiently represented.
To perform compression, DCT basis patches in Figure 5 are vectorized into a sequence of $P=64$ fixed basis vectors $\left\{ \mathbf{c}_{p}\right\} _{p=1}^{P}$ in the same manner as the input image blocks. Concatenating these patches column-wise into a matrix $\mathbf{C}$ and supposing there are $K$ blocks in the input image, denoting by $\mathbf{x}_{k}$ its $k^{th}$ vectorized block, to represent the entire image over the basis we solve $K$ linear systems of equations of the form
\begin{equation} \mathbf{C}\mathbf{w}_{k}=\mathbf{x}_{k} \end{equation}Each vector $\mathbf{w}_{k}$ in equation (9) stores the DCT coefficients (or weights) corresponding to the image block $\mathbf{x}_{k}$. Most of the weights in the coefficient vectors $\left\{ \mathbf{w}_{k}\right\} _{k=1}^{K}$ are typically quite small. Therefore, as illustrated by an example image in Figure 6 below, setting even $80\%$ of the smallest weights to zero gives an approximation that is essentially indistinguishable from the original image. Even setting $99\%$ of the smallest weights to zero gives an approximation to the original data wherein we can still identify the objects in the original image. To compress the image, instead of storing each pixel value, only these few remaining nonzero coefficients are kept.

Because the PCA optimization problem in (8) is convex in each variable $\mathbf{C}$ and $\mathbf{W}$ individually (but non-convex in both simultaneously) a natural approach to solving this problem is to alternately minimize (8) over $\mathbf{C}$ and $\mathbf{W}$ independently.
Beginning at an initial value for $\mathbf{C}^{\left(0\right)}$ this produces a sequence of iterates $\left(\mathbf{W}^{\left(i\right)},\,\mathbf{C}^{\left(i\right)}\right)$ where
\begin{equation} \begin{array}{c} \begin{aligned}\mathbf{W}^{\left(i\right)}=\,\, & \underset{\mathbf{W}}{\mbox{argmin}}\,\,\left\Vert \mathbf{C}^{\left(i-1\right)}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \\ \begin{aligned}\,\,\,\,\,\mathbf{C}^{\left(i\right)}=\,\, & \underset{\mathbf{C}}{\mbox{argmin}}\,\,\left\Vert \mathbf{C}\mathbf{W}^{\left(i\right)}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{array} \end{equation}and where each may be expressed in closed form.
Setting the gradient in each case to zero and solving gives
\begin{equation} \mathbf{W}^{\left(i\right)}=\left(\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{C}^{\left(i-1\right)}\right)^{\dagger}\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{X} \end{equation}and
\begin{equation} \mathbf{C}^{\left(i\right)}=\mathbf{X}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\left(\mathbf{W}^{\left(i\right)}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\right)^{\dagger} \end{equation}respectively, where $\left(\cdot\right)^{\dagger}$ denotes the pseudo-inverse. The procedure is stopped after taking a certain number of iterations and/or when the subsequent iterations do not change significantly.
1: Input: data matrix $\mathbf{X}$, initial $\mathbf{C}^{\left(0\right)}$, and maximum number of iterations $J$
2: for $\,\,i = 1,\ldots,J$
3: update the weight matrix $\mathbf{W}$ via $\mathbf{W}^{\left(i\right)}=\left(\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{C}^{\left(i-1\right)}\right)^{\dagger}\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{X}$
4: update the principal components matrix $\mathbf{C}$ via $\mathbf{C}^{\left(i\right)}=\mathbf{X}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\left(\mathbf{W}^{\left(i\right)}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\right)^{\dagger}$
5: end for
6: output: $\mathbf{C}^{\left(J\right)}$ and $\mathbf{W}^{\left(J\right)}$
While it is not obvious at first sight, there is also a closed-form solution to the PCA problem in (8) based on the Singular Value Decomposition (SVD) of the matrix $\mathbf{X}$. Denoting the SVD of $\mathbf{X}$ as $\mathbf{X}=\mathbf{U}\mathbf{S}\mathbf{V}^{T}$ this solution is given as
\begin{equation} \begin{array}{c} \,\,\,\,\,\,\,\,\,\,\,\mathbf{C}^{\star}=\mathbf{U}_{K}\mathbf{S}_{K,K}\\ \mathbf{W}^{\star}=\mathbf{V}_{K}^{T} \end{array} \end{equation}where $\mathbf{U}_{K}$ and $\mathbf{V}_{K}$ denote the matrices formed by the first $K$ columns of the left and right singular matrices $\mathbf{U}$ and $\mathbf{V}$ respectively, and $\mathbf{S}_{K,K}$ denotes the upper $K\times K$ sub-matrix of the singular value matrix $\mathbf{S}$. Notice that since $\mathbf{U}_{K}$ is an orthogonal matrix the recovered basis (for the low dimensional subspace) is indeed orthogonal.
Here we show how to derive PCA from a different perspective, as the orthogonal directions of largest variance in data. While this perspective is not particularly useful when using PCA as a preprocessing technique (since all we care about is reducing the dimension of the feature space, and so any basis spanning a proper subspace will suffice), it is often used in exploratory data analysis in fields like statistics and the social sciences (see e.g., factor analysis).
Adopting the same notation as in Subsection 1.1, we have a dataset of $P$ points $\left\{ \mathbf{x}_{p}\right\} _{p=1}^{P}$ - each of dimension $N$. Given a unit direction $\mathbf{d}$, we can calculate the variance of data in that direction (i.e., how much the dataset spreads out in that direction) as the average squared inner product of the data against $\mathbf{d}$
\begin{equation} \frac{1}{P}\underset{p=1}{\overset{P}{\sum}} \left(\mathbf{d}^T\mathbf{x}_{p}\right) ^{2} \end{equation}Putting data points as columns into a matrix $\mathbf{X}$ as in equation (6), this can be written more compactly as
\begin{equation} \frac{1}{P}\Vert\mathbf{X}^{T}\mathbf{d}\Vert_{2}^{2}=\frac{1}{P}\mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d} \end{equation}With the expression in (15) at hand, we can find the unit direction $\mathbf{d}$ which maximizes it. This direction will be, by definition, the direction of maximum variance in data.
Let us assume that the $N\times N$ symmetric positive semi-definite matrix $\mathbf{X}\mathbf{X}^{T}$ has eigenvalues $\lambda_{1}\geq\lambda_{2}\geq\cdot\cdot\cdot\geq\lambda_{N}\geq0$ and corresponding eigenvectors $\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{N}$, with an eigen-decomposition
\begin{equation} \mathbf{X}\mathbf{X}^{T}=\mathbf{A}\boldsymbol{\Lambda}\mathbf{A}^{T} \end{equation}where $\mathbf{A}$ is an orthonormal basis whose columns are the eigenvectors, and $\boldsymbol{\Lambda}$ is a diagonal matrix with the corresponding eigenvalues along its diagonal. With this eigen-decomposition we can write
\begin{equation} \mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d}=\mathbf{d}^{T}\mathbf{A}\boldsymbol{\Lambda}\mathbf{A}^{T}\mathbf{d}=\mathbf{r}^{T}\boldsymbol{\Lambda}\mathbf{r} \end{equation}where $\mathbf{r}=\mathbf{A}^{T}\mathbf{d}$.
Expressing $\mathbf{r}^{T}\boldsymbol{\Lambda}\mathbf{r}$ in terms of individual entries in $\mathbf{r}$ and $\boldsymbol{\Lambda}$ we have
\begin{equation} \mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d}={\sum}_{n=1}^N\lambda_{n}r_{n}^{2}\leq{\sum}_{n=1}^N\lambda_{1}r_{n}^{2}=\lambda_{1}\Vert\mathbf{r}\Vert_{2}^{2}=\lambda_{1}\mathbf{d}^{T}\mathbf{A}\mathbf{A}^{T}\mathbf{d}=\lambda_{1}\mathbf{d}^{T}\mathbf{d}=\lambda_{1} \end{equation}where we use the fact that $\mathbf{A}$ is an orthonormal basis and $\mathbf{d}$ has unit length.
Notice, if you set $\mathbf{d}=\mathbf{a}_{1}$ then the objective meets its upper bound in (18), since
\begin{equation} \mathbf{a}_{1}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{a}_{1}=\mathbf{a}_{1}^{T}\mathbf{A}\boldsymbol{\Lambda}\mathbf{A}^{T}\mathbf{a}_{1}=\mathbf{e}_{1}^{T}\mathbf{\boldsymbol{\Lambda}e}_{1}=\lambda_{1} \end{equation}where $\mathbf{e}_{1}=\left[\begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0\end{array}\right]^{T}$ is the first standard basis vector, and we indeed have that
\begin{equation} \begin{aligned}\,\,\,\,\,\mathbf{a}_{1}=\,\, & \underset{\Vert\mathbf{d}\Vert_{2}=1}{\mbox{argmax}}\,\,\mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d} \end{aligned} \end{equation}A similar approach can be taken to find the second largest direction of variance of the matrix $\mathbf{X}\mathbf{X}^{T}$, i.e., the unit vector $\mathbf{d}$ that maximizes the value of $\mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d}$ but where $\mathbf{d}$ is also orthogonal to $\mathbf{a}_1$ - the first largest direction of variance.
We now write the inequality in (18), slightly differently, as
\begin{equation} \mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d}=\lambda_{1}r_{1}^{2}+{\sum}_{n=2}^N\lambda_{n}r_{n}^{2}\leq\lambda_{2}r_{1}^{2}+{\sum}_{n=2}^{N}\lambda_{2}r_{n}^{2}={\sum}_{n=1}^{N}\lambda_{2}r_{n}^{2} \end{equation}where the inequality holds since we are only looking for directions perpendicular to $\mathbf{a}_{1}$, therefore $r_{1}=\mathbf{d}^{T}\mathbf{a}_{1}=0$, and we also have that $\lambda_{2}\geq\cdot\cdot\cdot\geq\lambda_{N}\geq0$ by assumption.
Hence, we have
\begin{equation} \mathbf{d}^{T}\mathbf{X}\mathbf{X}^{T}\mathbf{d}\leq{\sum}_{n=1}^{N}\lambda_{2}r_{n}^{2}=\lambda_{2}\Vert\mathbf{r}\Vert_{2}^{2}=\lambda_{2}\mathbf{d}^{T}\mathbf{A}\mathbf{A}^{T}\mathbf{d}=\lambda_{2}\mathbf{d}^{T}\mathbf{d}=\lambda_{2} \end{equation}Notice, this time, the upper bound is met with $\mathbf{d}=\mathbf{a}_{2}$.
Similarly, we can show that the rest of the orthogonal directions of maximum variance in data are the remaining eigenvectors of $\mathbf{X}\mathbf{X}^{T}$, which are precisely the singular value solution given previously in equation (13).
To see why this is true, we expand $\mathbf{XX}^{T}$ using its singular value decomposition $\mathbf{X}=\mathbf{U}\boldsymbol{S}\mathbf{V}^{T}$
Given the eigen-decomposition of $\mathbf{X}\mathbf{X}^{T}$ as $\mathbf{X}\mathbf{X}^{T}=\mathbf{A}\boldsymbol{\Lambda}\mathbf{A}^{T}$ in equation (16), a simple inspection reveals that $\mathbf{U}=\mathbf{A}$ and $\mathbf{S}\mathbf{S}^{T}=\boldsymbol{\Lambda}$.