Press the botton 'Toggle code' below to toggle code on and off for entire this presentation.
from IPython.display import display
from IPython.display import HTML
import IPython.core.display as di # Example: di.display_html('<h3>%s:</h3>' % str, raw=True)
# This line will hide code by default when the notebook is exported as HTML
di.display_html('<script>jQuery(function() {if (jQuery("body.notebook_app").length == 0) { jQuery(".input_area").toggle(); jQuery(".prompt").toggle();}});</script>', raw=True)
# This line will add a button to toggle visibility of code blocks, for use with the HTML export version
di.display_html('''<button onclick="jQuery('.input_area').toggle(); jQuery('.prompt').toggle();">Toggle code</button>''', raw=True)
1. How do we define the derivative driven tangent line?¶
Remember what we said in words / pictures previously about the derivative of a function at a point: the derivative at a point defines a line that is always tangent to a function, encodes its steepness at that point, and generally matches the underlying function near the point locally. In other words: the derivative at a point is the slope of the tangent line there.
The derivative at a point is the slope of the tangent line at that point.
How can we more formally describe such a tangent line and derivative?
1.1 Secant lines¶
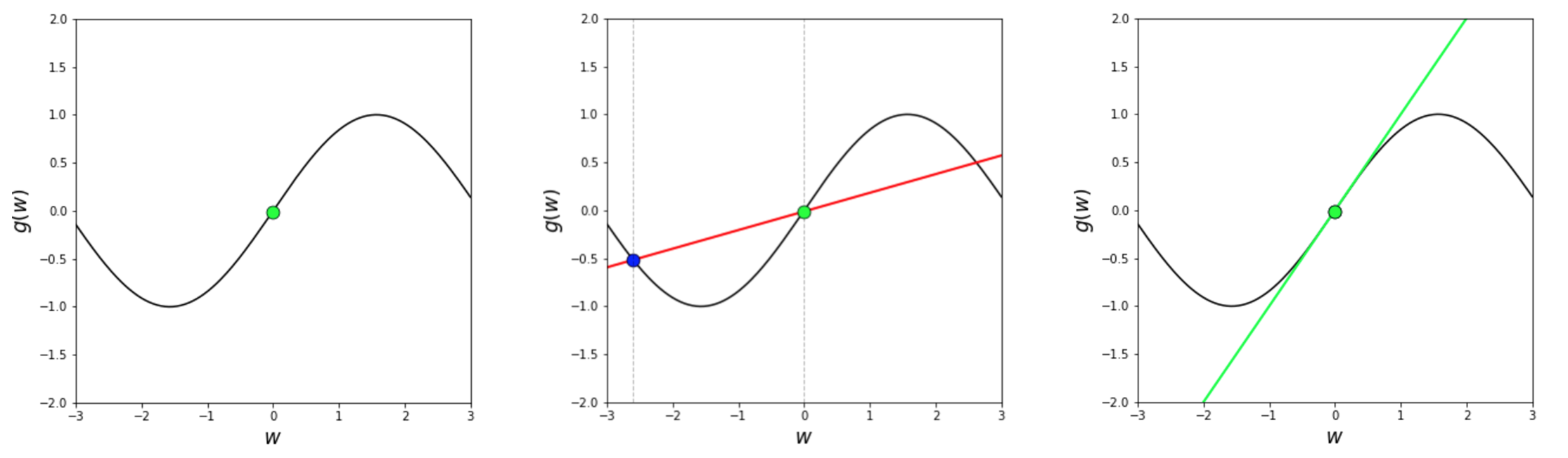
- (left panel) simple sinusoid with the point $(w_0,g(w_0)) = (0, \text{sin}(0))$ colored green
- (middle panel) another point $(w_1,g(w_1)) = (-2.6, \text{sin}(-2.6))$ shown in blue and the *secant line* connecting two points in red
- (right panel) the tangent line at $w_0 = 0$ in green

- A secant line is just a line formed by taking any two points on a function - like our sinusoid - and connecting them with a straight line.
- A tangent line can cross through several points of a function it is explicitly defined using only a single point.
- So in short - a secant line is defined by two points, a tangent line by just one.
The equation of a secant line¶
- all we need is the slope and any point on the line to define it
- the slope of a line can be found using any two points on it (like the two points we used to define the secant to begin with)
The slope - the line's 'steepness' or 'rise over run' - is the ratio of change in output $g(w)$ over the change in input $w$. For two points $w_0$ and $w_1$ it is
\begin{equation} \text{slope of a secant line} = \frac{g(w^1) - g(w^0)}{w^1 - w^0} \end{equation}- equation of secant line
Example 1. Secant line computation¶

With $w^0 = 0$ and $w^1 = -2.6$
\begin{equation} h(w) = \text{sin}(0) + \frac{\text{sin}(-2.6) - \text{sin}(0)}{-2.6 - 0}(w - 0) \end{equation}- approximately the line
1.2 From secant to tangent line¶
- the tangent line at $w_0$ formed by secant line passing through $\left(w_0,g\left(w_0\right)\right)$ and $\left(w_1,g\left(w_1\right)\right)$, and pushing $w_1$ towards $w_0$ from both left and right until $w_1 \approx w_0$
- the next slider widget illustrates precisely this idea
# what function should we play with? Defined in the next line, along with our fixed point where we show tangency.
g = lambda w: np.sin(w)
# create an instance of the visualizer with this function
st = calclib.secant_to_tangent.visualizer(g = g)
# run the visualizer for our chosen input function and initial point
st.draw_it(w_init = 0, num_frames = 200)