Motivation:¶
$\boxed{1}$ In many modern applications of machine learning, data is high-dimensional, producing:
- computational problems in the training of predictive models
- harder to interpret models
PCA is a classical technique for reducing the feature dimension of a given dataset.
$\boxed{2}$ PCA presents a fundamental mathematical archetype, the matrix factorization, that provides a useful way of organizing our thinking about a wide array of important learning models.
Press the button 'Toggle code' below to toggle code on and off for entire this presentation.
from IPython.display import display
from IPython.display import HTML
import IPython.core.display as di # Example: di.display_html('<h3>%s:</h3>' % str, raw=True)
# This line will hide code by default when the notebook is exported as HTML
di.display_html('<script>jQuery(function() {if (jQuery("body.notebook_app").length == 0) { jQuery(".input_area").toggle(); jQuery(".prompt").toggle();}});</script>', raw=True)
# This line will add a button to toggle visibility of code blocks, for use with the HTML export version
di.display_html('''<button onclick="jQuery('.input_area').toggle(); jQuery('.prompt').toggle();">Toggle code</button>''', raw=True)
1. Principal Component Analysis¶
PCA works by simply projecting the data onto a suitable lower dimensional feature subspace, that is one which hopefully preserves the essential geometry of the original data. This subspace is found by determining one of its spanning sets (e.g., a basis) of vectors which spans it.
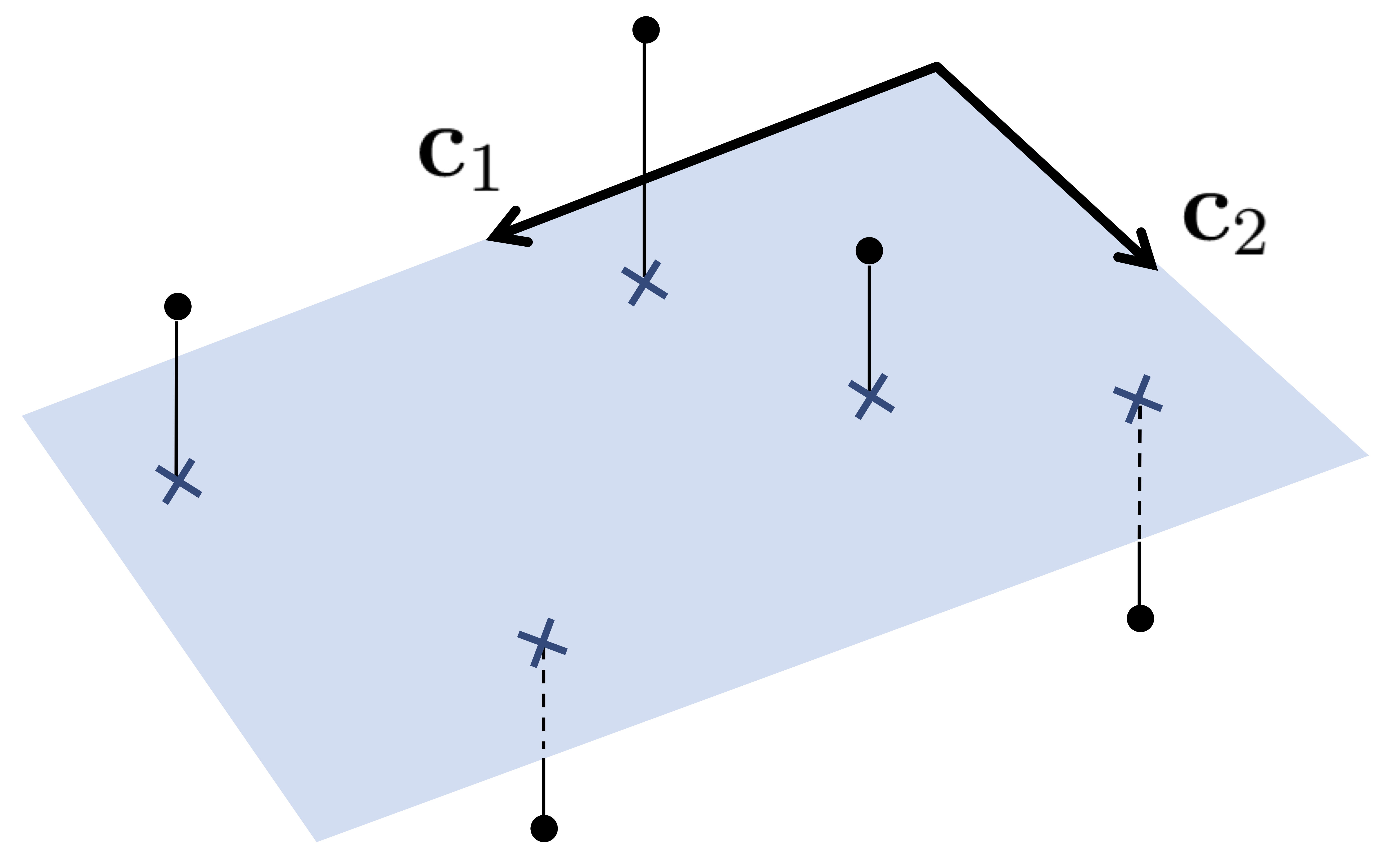
1.1 Notation and modeling¶
Suppose that we have $P$ data points $\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{P}$, each of dimension $N$.
The goal with PCA is, for some user chosen dimension $K<N$, to find a set of $K$ vectors $\mathbf{c}_{1}, \mathbf{c}_{2}, \dots, \mathbf{c}_{K}$ that represent the data fairly well.
Put formally, we want for each $p=1, 2, \ldots, P$ to have
\begin{equation} \underset{k=1}{\overset{K}{\sum}}\mathbf{c}_{k}w_{k,p}\approx\mathbf{x}_{p} \end{equation}Stacking the desired spanning vectors column-wise into the $N\times K$ matrix $\mathbf{C}$ as
\begin{equation} \mathbf{C}=\left[\begin{array}{cccc} \mathbf{c}_{1} & \mathbf{c}_{2} & \cdots & \mathbf{c}_{K}\end{array}\right] \end{equation}and denoting
\begin{equation} \mathbf{w}_{p}=\left[\begin{array}{c} w_{1,p}\\ w_{2,p}\\ \vdots\\ w_{K,p} \end{array}\right] \end{equation}we have, for each $p$, that
\begin{equation} \mathbf{C}\mathbf{w}_{p}\approx\mathbf{x}_{p} \end{equation}More compactification! Denote the $K\times P$ weight matrix
\begin{equation} \mathbf{W}=\left[\begin{array}{cccc} \mathbf{w}_{1} & \mathbf{w}_{2} & \cdots & \mathbf{w}_{P}\end{array}\right] \end{equation}and the $N\times P$ data matrix
\begin{equation} \mathbf{X}=\left[\begin{array}{cccc} \mathbf{x}_{1} & \mathbf{x}_{2} & \cdots & \mathbf{x}_{P}\end{array}\right] \end{equation}to write all $P$ approximate equalities of the form $\mathbf{C}\mathbf{w}_{p}\approx\mathbf{x}_{p}$ more compactly (in a single equation) as
\begin{equation} \mathbf{C}\mathbf{W}\approx\mathbf{X} \end{equation}The goal of PCA: learn matrices $\mathbf{C}$ and $\mathbf{W}$ such that
\begin{equation} \mathbf{C}\mathbf{W}\approx\mathbf{X} \end{equation}This naturally leads to determining $\mathbf{C}$ and $\mathbf{W}$ by minimizing the following \begin{equation} \begin{aligned}\underset{\mathbf{C},\mathbf{W}}{\mbox{minimize}} & \,\,\,\,\,\left\Vert \mathbf{C}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{equation}
Example 1: PCA on simulated data¶
Example 2: PCA and classification data¶
While PCA can technically be used for preprocessing data in a predictive modeling scenario, it can cause severe problems in the case of classification, by completely destroying the separation structure.
Example 3: Role of efficient bases in digital image compression¶
In a typical image compression scheme an input image is first cut up into small square (typically $8 \times 8$ pixel) blocks. The values of pixels in each block are stacked into a column vector $y$, and compression is then performed on these individual vectorized blocks.
The basic idea: with specific bases like DCT (left panel - used in JPEG), we only need very few of their elements to very closely approximate any natural image. This is because each DCT basis element represents a fluctuation commonly seen across the entirety of a natural image block. The same cannot be said of other bases with more locally defined elements like the standard basis shown on the right.

What is the difference between PCA and JPEG image compression?
Even though we're still aiming to reduce the dimension of data, instead of seeking out a basis (as with PCA), here we have a fixed basis (DCT) over which image data can be very efficiently represented.
In other words, denoting by $\mathbf{x}_{k}$ the $k^{th}$ (vectorized) image block, we solve $K$ linear systems of the form
\begin{equation} \mathbf{C}\mathbf{w}_{k}=\mathbf{x}_{k} \end{equation}where $\mathbf{C}$ is known (and no longer learned).
After solving $\mathbf{C}\mathbf{w}_{k}=\mathbf{x}_{k}$, most of the weights in the found coefficient vector $\mathbf{w}_{k}$ are typically quite small - so we set them to zero.

1.2 Optimization of the PCA problem¶
Recall the PCA optimization problem:
\begin{equation} \begin{aligned}\underset{\mathbf{C},\mathbf{W}}{\mbox{minimize}} & \,\,\,\,\,\left\Vert \mathbf{C}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{equation}- This problem is convex in each variable $\mathbf{C}$ and $\mathbf{W}$ individually but non-convex in both simultaneously.
- We solve it via alternation minimization: alternately keep one variable fix and solve for the other.
Beginning at an initial value for $\mathbf{C}=\mathbf{C}^{\left(0\right)}$, we find $\mathbf{W}^{\left(1\right)}$ as
\begin{equation} \begin{array}{c} \begin{aligned}\mathbf{W}^{\left(1\right)}=\,\, & \underset{\mathbf{W}}{\mbox{argmin}}\,\,\left\Vert \mathbf{C}^{\left(0\right)}\mathbf{W}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{array} \end{equation}Setting the gradient to zero, this has a closed form solution given by
\begin{equation} \mathbf{W}^{\left(1\right)}=\left(\left(\mathbf{C}^{\left(0\right)}\right)^{T}\mathbf{C}^{\left(0\right)}\right)^{\dagger}\left(\mathbf{C}^{\left(0\right)}\right)^{T}\mathbf{X} \end{equation}where $\left(\cdot\right)^{\dagger}$ denotes the pseudo-inverse.
Keeping $\mathbf{W}$ fixed at $\mathbf{W}^{\left(1\right)}$, we now minimize the PCA cost over $\mathbf{C}$, giving
\begin{equation} \begin{aligned}\,\,\,\,\,\mathbf{C}^{\left(1\right)}=\,\, & \underset{\mathbf{C}}{\mbox{argmin}}\,\,\left\Vert \mathbf{C}\mathbf{W}^{\left(1\right)}-\mathbf{X}\right\Vert _{F}^{2}\end{aligned} \end{equation}with the closed form solution given by
\begin{equation} \mathbf{C}^{\left(1\right)}=\mathbf{X}\left(\mathbf{W}^{\left(1\right)}\right)^{T}\left(\mathbf{W}^{\left(1\right)}\left(\mathbf{W}^{\left(1\right)}\right)^{T}\right)^{\dagger} \end{equation}This procedure is repeated, and only stopped after taking a certain number of iterations and/or when the subsequent iterations do not change significantly.
Alternating minimization algorithm for PCA¶
1: Input: data matrix $\mathbf{X}$, initial $\mathbf{C}^{\left(0\right)}$, and maximum number of iterations $J$
2: for $\,\,i = 1,\ldots,J$
3: update the weight matrix $\mathbf{W}$ via $\mathbf{W}^{\left(i\right)}=\left(\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{C}^{\left(i-1\right)}\right)^{\dagger}\left(\mathbf{C}^{\left(i-1\right)}\right)^{T}\mathbf{X}$
4: update the principal components matrix $\mathbf{C}$ via $\mathbf{C}^{\left(i\right)}=\mathbf{X}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\left(\mathbf{W}^{\left(i\right)}\left(\mathbf{W}^{\left(i\right)}\right)^{T}\right)^{\dagger}$
5: end for
6: output: $\mathbf{C}^{\left(J\right)}$ and $\mathbf{W}^{\left(J\right)}$
The SVD solution¶
Denoting the singular value decomposition of $\mathbf{X}$ as $\mathbf{X}=\mathbf{U}\mathbf{S}\mathbf{V}^{T}$, a closed form solution to the PCA problem can be found as
\begin{equation} \begin{array}{c} \,\,\,\,\,\,\,\,\,\,\,\mathbf{C}^{\star}=\mathbf{U}_{K}\mathbf{S}_{K,K}\\ \mathbf{W}^{\star}=\mathbf{V}_{K}^{T} \end{array} \end{equation}where $\mathbf{U}_{K}$ and $\mathbf{V}_{K}$ denote the matrices formed by the first $K$ columns of the left and right singular matrices $\mathbf{U}$ and $\mathbf{V}$ respectively, and $\mathbf{S}_{K,K}$ denotes the upper $K\times K$ sub-matrix of the singular value matrix $\mathbf{S}$.