About us¶

- Adjunct Professors in EECS department
- where we both earned our PhDs

- Authors of Machine Learning Refined (Cambridge University Press) - www.mlrefined.com
- Used in EECS 396, 496: Machine Learning: Foundations, Applications, and Algorithms
- Notes from this class based on *new* material for 2nd edition!

- Owners of local deep learning consultancy Degree Six - www.dgsix.com
- We help everyone from startups to established businesses develop AI-fueled products and build machine learning / deep learning teams
About the course¶
Optimization is the workhorse of machine learning / deep learning¶
Every way we know how to learn fundamentally requires mathematical optimization¶
- Supervised learning: parameters must be properly tuned in order to represent data / make accurate predictions
- e.g., linear supervised learning, deep neural networks, random forests, kernel methods,...- Unsupervised learning: parameters must be properly tuned in order to reduce the dimnension of data properly
- e.g., PCA, K-Means, Recommender Systems,...- Reinforcement Learning: large state spaces (e.g., for Atari games) require repeated use of supervised learning
- Deep Q-Learning, Policy-gradient methods,...What is mathematical optimization?¶
- Every machine learning / deep learning learning problem has parameters that must be tuned properly to ensure optimal learning.
- e.g., two parameters to tune (slope and intercept) in simplest instance of linear regression - we fit a line to data
- These parameters are tuned by forming what is called a cost function or loss function
- Proper tuning of weights corresponds geometrically to minimizing the cost function
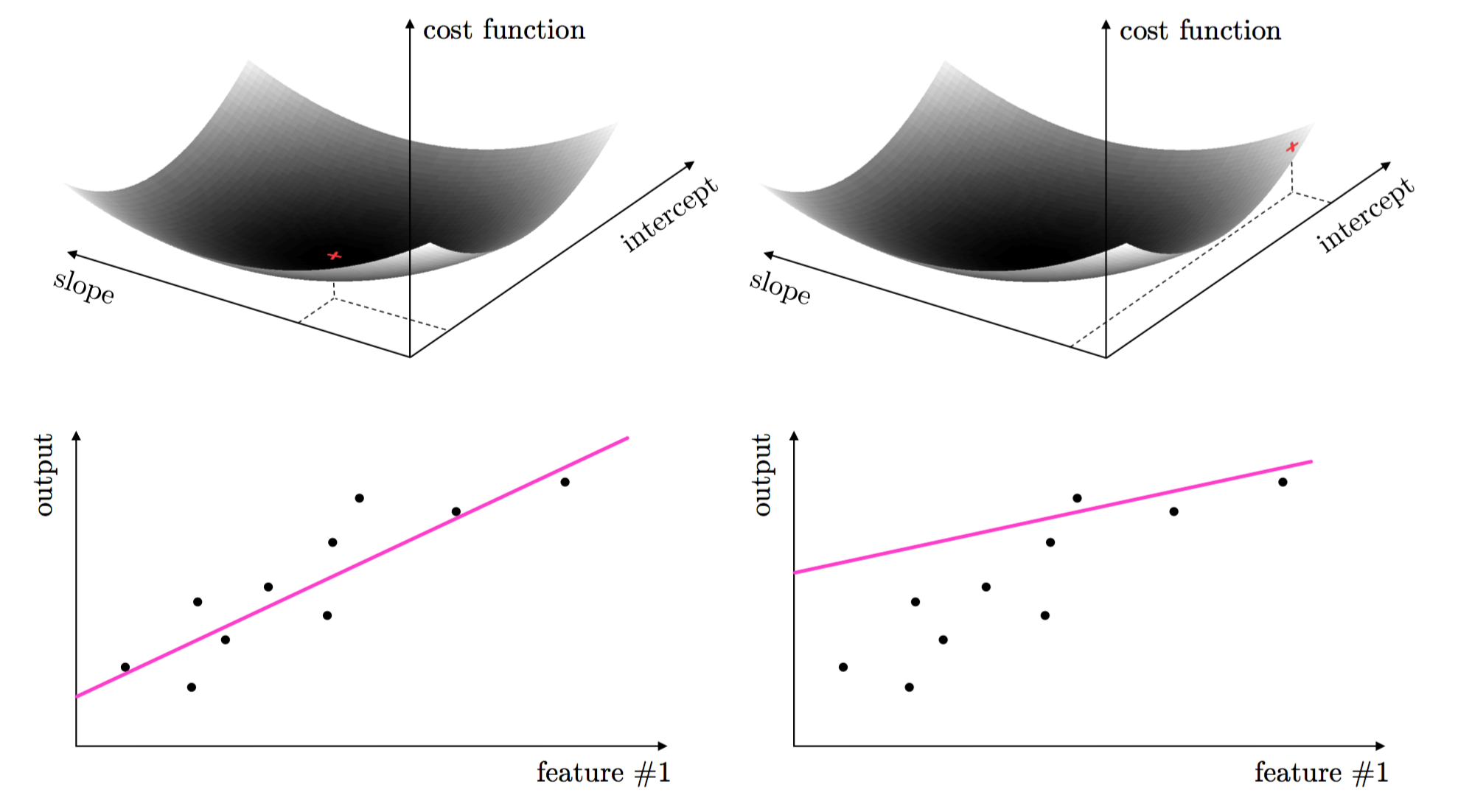
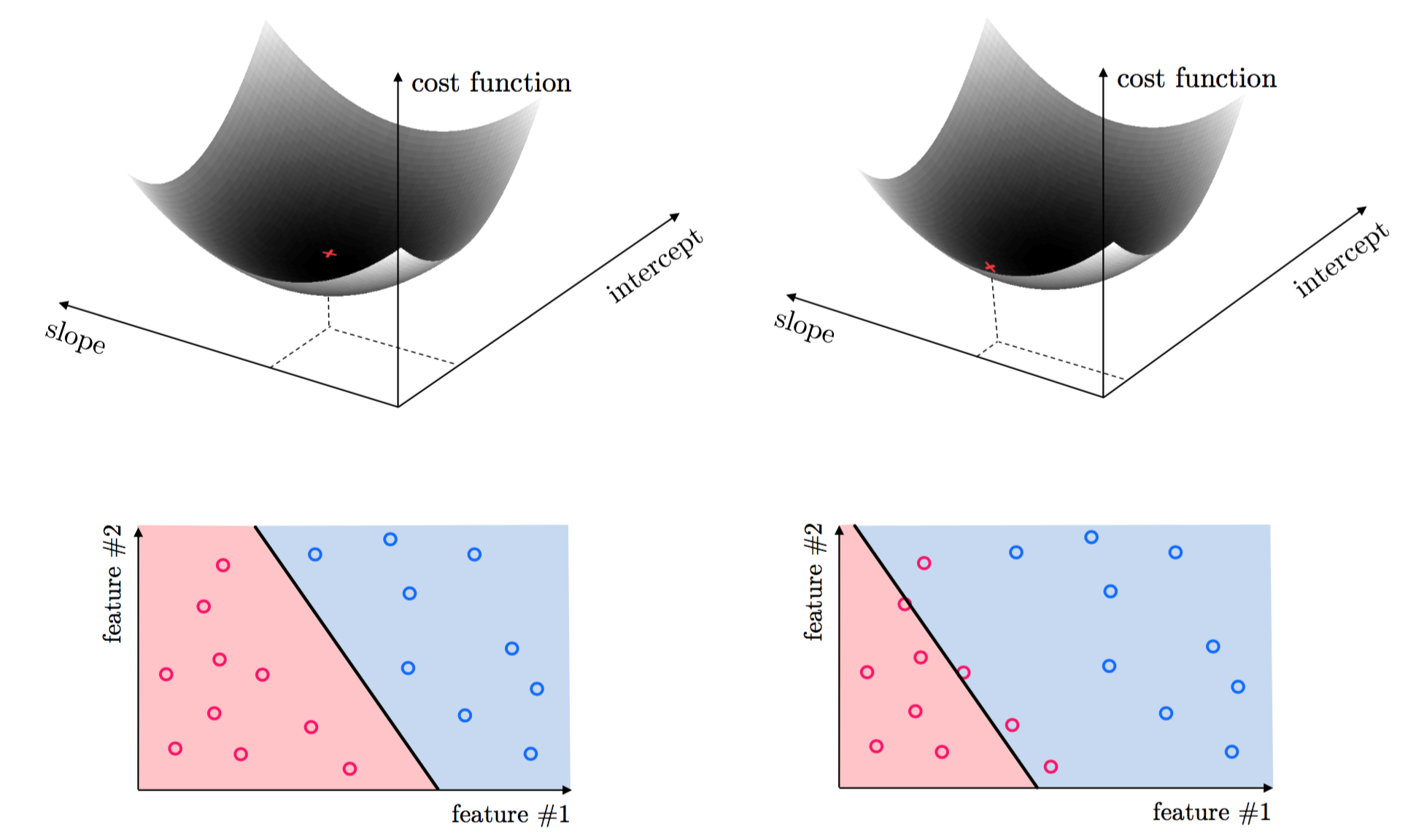
What is mathematical optimization?¶
- mathematical optimization is the set of tools designed to find such minima
- the algorithms are iterative in nature (few closed form solutions)
- the algorithms are based on fundamental principles from calculus and geometry
Course topics¶
Course topics¶
1) Computational calculus part 1
- mathematical functions, function arithmetic, the computation graph
- derivative rules, numerical differentiation, automatic differentiation
- the first order condition and alternating descent2) Optimization and Unsupervised Learning
- eigenvalues / eigenvectors and the power method
- PCA, random projections, LDA, Recommender Systems
- K-Means, Nonnegative Matrix Factorization, Sparsity, and other clustering methods3) Computational calculus part 2
- hyperplanes and high dimensional quadratics
- second derivatives and curvature
- Taylor series, higher order derivatives and computationCourse topics¶
4) First and second order methods
- global and random local search
- gradient descent, normalized and unnormalized forms
- steepest descent variations, steplength rules, stochastic methods
- Newton's method, non-convex adjustments, quasi-Newton's method5) Optimization and supervised learning
- linear supervised methods
- deep neural networks, specialized first order methods (RProp, RMSprop, ADAM, noisy gradient)
- boosted trees and heuristic methodsLogistics¶
Logistics¶
- All slides and notes will be posted to https://jermwatt.github.io/mlrefined
- pull this repo and keep it up to date
- We may use a Piazza page for class forum discussion
- Office hours: 12 - 1pm Mon/Wed in Annenberg Hall room G21 (starting second week of class)
- Assignments: 5 homeworks (75% of final grade), 1 individual project (25% of final grade)
- All assignments must be completed using Python 3 Jupyter notebooks, turned in on canvas (no hard copy)
- Late homework = 1% off every hour late starting at end of due class
Prerequisites¶
Prerequisites¶
- Expert Google-ing skills
- You understand how to / the value of Google and Stack overflow
- Basic familiarity with Linear Algebra and Calculus
- We will review, so OK if rusty
- Basic familiarity with fundamental machine learning concepts
- We will review as we go along, so OK if rusty
- Strong familiarity with the Python programming language
- functions / classes (i.e,. basic familiarity with object oriented programming)
- We will not review, play catch-up: e.g., https://www.codecademy.com/
- Familiarity with using Jupyter notebook enviro for prototyping
- If unfamiliar easy to catch-up: see e.g., https://www.youtube.com/watch?v=HW29067qVWk&t=639s
- Familiarity with github
- if unfamiliar, make yourself an account and easy catch-up: see e.g., https://www.youtube.com/watch?v=SWYqp7iY_Tc